六年级上册《比》这一单元紧随着分数除法的学习，也在大多数学校期中考试的考试范围。比的基础知识点并不是很多，但是需要理解透彻，用起来就能得心应手。

一、比的意义

1、比：两个数相除又叫做两个数的比。比表示的两个数之间的相除关系。

2、比的结构：在两个数的比中，比号前面的数叫比的前项，比号后面的数叫比的后项。

比的前项除以后项所得的商，叫做比值。比值通常用分数表示，也可以用小数或整数表示。

最简比：比的前项和后项都是整数且只有公因数1，这样的比称为最简整数比。

3、比可以表示两个同类数量之间的倍数关系：比如一个长方形长和宽的比是15：10；

也可以表示两个不同类数量之间的相除关系，得到一个新的量：比如路程÷时间=速度。

4、求比值：

比的前项除以后项所得的商叫做比值，所以用比的前项除以后项即可求得比值。

比值是一个具体的数，通常用分数表示，也可以用小数或整数表示。

• 比值是否带单位：同类数量的比仅表示数量之间的倍数关系，其比值不带单位；
• 不同类数量的比，其比值是一个新的数量，通常带一个复合单位（如 速度）。

5、比与比值的关系：二者在写法上可能相同（都可以用分数表示），但比表示两个数量之间的相除关系；比值则是一个具体的数字。

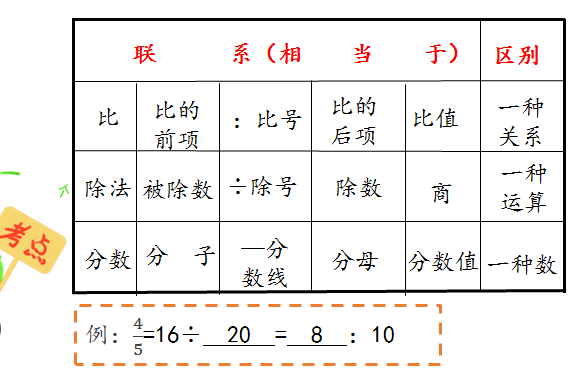
6、比、除法与分数之间的联系：a:b=a÷b=a/b（b≠0）

比、除法与分数之间的区别：

• （1）、意义不同：比表示两个数量之间的相除关系；除法是一种运算；分数是一个数；
• （2）、表示方法不同：除法是一种运算，只能用算式表示；比和分数都可以用分数的形式表示，但是分数并不一定表示两个数量的比。
• （3）、结果不同：除法的计算结果是一个商，这个商可以是整数、小数或分数；比只有当要求比值的时候，才需要用除法计算，比值可以用整数、小数或分数表示；而分数就是一个数，不需要计算。

7、为什么比的后项不能为0：在除法中，除数不能为0；在分数中，分母不能为0；而比的后项就相当于除法中的除数、分数中的分母，所以比的后项也不能为0。

8、求比中的未知项：

• （1）、在除法中，被除数÷除数=商，这3个数量只要知道其中任意2个量，就能求出另一个量。除数=被除数÷商；被除数=商×除数。
• （2）、比和除法本质上相通的，也就是说，比的前项、后项以及比值中的任意两个量，就能求出另一个量。前项=后项×比值；后项=前项÷比值；比值=前项÷后项。

9、体育比赛中的比分，与数学的中比有什么区别？

• （1）、体育比赛中的比表示的仅仅是比赛双方的得分情况，比如3：2或11：9等等，也就可以是2：0或0：3甚至是0：0，这个得分的比表示的不是两个数的相除关系，而是双方得分的相差关系，比号的前后和后面都可以是0。
• （2）、而数学中的比表示的是两个数之间的相除关系，其后项是不能等于0的。比可以计算出相除的结果（也就是比值），也可以进行化简，如3：6=1：2。但是比赛得分就不能除法计算，也不能化简。

二、比的基本性质与化简比

1、比的基本性质：比的前项和后项同时乘或除以相同的数（0除外），比值不变。

根据比与除法、分数之间的关系，可以类比一下比的基本性质、除法中的商不变性质、分数的基本性质。

• 商不变性质：被除数和除数同时乘或除以相同的数（0除外），商不变；
• 分数的基本性质：分数的分子和分母同时乘或除以相同的数（0除外），分数大小不变。

2、化简比：利用比的基本性质，把比化简成最简整数比。

最简整数比：比的前项和后项都是整数，且只有公因数1，也就是比的前项和后项互质。

3、化简比的方法总结：

• （1）、整数比化简：前项和后项同时除以他们的最大公因数；
• （2）、分数比化简：前项和后项同时乘以分母的最小公倍数，使其变成整数比，再按整数比的方法化简；
• （3）、小数比化简：前项和后项的小数点同时向右移动相同的位数，使其变成整数比，再按整数比的方法化简；
• （4）、小数和分数混合的比：可以先把小数化成分数，使其变成分数比，再按分数比的方法化简；也可以是先把分数化成小数，使其变成小数比，再按小数比的方法化简。

三、利用比的基本性质解题

1、常考题型一：例、把5：12的前项加上5，要使其比值不变，后项应该加上多少？

【解析】误区提示：比的基本性质是比的前项和后项同时乘或除以相同的数（0除外），比值不变。如果把比的比的前项和后项同时加上或者减去相同的数（0除外），并不能保证比值不变，所以后项不能和前项一样加上5。

正确思路：前项加上5，5+5=10，相当于前项乘以2，要使其比值不变，后项也要乘以2，12×2=24，5：12=10：24。但是题目问的时候后项应该加上多少，所以24-12=12，后项应该加上12。

2、常考题型二：化连比。

例、已知甲数：乙数=3：10，乙数：丙数=4：9，请问甲乙丙三个数的比是多少？

【解析】甲数：乙数=3：10，乙数：丙数=4：9，可以发现甲乙的比中乙数占10份，而乙丙的比中乙数占4份，同一个数在不同的比中的份数不一样，是因为每一份的量不统一。那么咱们可以抓住乙数这个中间量来统一每份数。

具体方法就是找到中间量的最小公倍数，4 和10的最小公倍数是20，根据比的基本性质，甲数：乙数=3：10=6：20；乙数：丙数=4：9=20：45。

这样一来乙数在两个比中所占的份数都是20份，那么两个比中的每一份的量就是相同的，可以写成连比，甲：乙：丙=6：20：45。

本期思考题：甲数是乙数的3/10，乙数是丙数的4/9，求这三个数的连比。