微分和导数是一回事吗（微分、导数是怎么回事?）

有

一、先复习已经学过的分数、速度

1、小学阶段学过分数

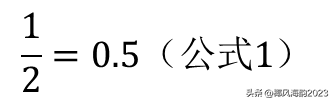
为了方便后面的对比理解，我们先明确以下概念：在上面的分数中，数字1称做分子，数字2称做分母，数字0.5称做分数值；

把公式1变化一下，写成

0.5×2=1 或者1=0.5×2 （公式2）

称呼随之改变：数字1在这里称做积，数字2称做乘数，数字0.5称做被乘数。

从以上两个公式的情形可以看出来，实质内容一样的东西，表达的形式变了，称呼也跟着变了。俗话说入乡随俗，到哪道山唱什么歌，大家要慢慢习惯这个做法。

其实严格说来，细论的话，不同的表达形式，表征的内涵是不完全相同的，这就是表达形式和称呼变化的根据。比如公式1，表达的是一个东西分成两份，每份分了多少；公式2又有两种表达方式，前者表达的是两个0.5合起来是1，后者表达的是1分成了两个0.5。

2、初中阶段学过有关速度公式

用符号表示，则有

公式4与公式3在物理上完全一样，那为什么非要用符号表达呢？

在科学上，常用各种符号表达各种概念、公式、数值等，这种做法一是约定俗成，大家都这么做的，我们只用记住、使用就行；二是方便与人沟通、交流；三是为了表达简洁，方便推导运算。

二、下面，我们稍微扩展一点距离、时间的表示方法。

1、距离：假设你在操场上沿跑道跑步，从100米处跑到了300米处，跑的距离是200米。

现在沿跑道做一数轴，起跑处取为原点，把跑道100米处记为x1，把300米处记为x2，则你跑的距离S= x2-x1=300-100=200（米）

由于S是x2与x1的差值，那我们就换个记法，这个差值不再用字母S表示，而是用Δx，即Δx= x2-x1=300-100=200（米）。其中Δ是希腊字母，英语词是Delta，音译读作：德尔塔。

在这里，需要明确指出，由于Δx= 200米是一个确定的差值，故，我们说符号Δ表示的是一个有限大小的差值。（注意“有限大小”这个说法，后面要对比使用的）

2、时间：假设你从100米处开始跑，时间是9点50分29秒，跑到300米处的时间是9点50分59秒，即你跑200米用了30秒的时间，也即t=30秒。

与距离一样，我们换个记法：t1=9点50分29秒，t2=9点50分59秒，Δt= t2- t1=9点50分59秒-9点50分29秒=30秒

至此，我们知道，公式4可以改写成如下形式

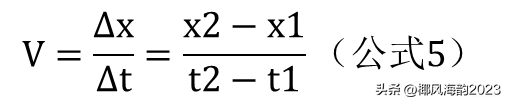
三、平均速度、瞬时速度

1、上面的公式计算出来的速度，是在30秒内跑200米的平均速度。

你在跑步时，实际上可能会忽快忽慢，甚至会停下来喘口气。平均速度的意思就是，不管你怎样跑，反正是跑了200米，用了30秒，相当于你用平均速度匀速跑了30秒。

2、那你的起跑速度如何呢？

起跑速度就是在起跑时刹那间的速度，物理上称为瞬时速度。

设想你跑了很多次，跑的距离越来越短，用的时间自然也是越来越少。

极端情况：你跑的距离是无限短，用的时间是无限少，这个时候你的速度就是起跑速度。

注意“无限短、无限少”这种说法，对比前面的“有限大小”的说法，加以体会、理解“有限小、无限小”两个词汇表达的意义。

四、无穷小

“有限小”好理解，我就不再啰嗦了。那么，什么是“无限小”、怎么理解“无限小”这个概念呢？

借用友友的精妙解释：“包子的馅趋于无限小时等于馒头，包子的皮趋于无限小时等于丸子”。无限小，也称作无穷小。

前面我们知道，对“有限大小”的值，用字母Δ表示，现在对于“无穷小”，自然不能继续再用Δ表示。字母Δ英语词汇是delta，我们就用这个词汇的第一个字母d表示“无穷小”。

这样，对于起跑速度，也即起跑时的瞬时速度，公式5可以改写成

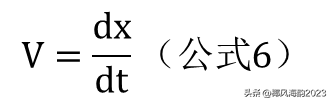
上式表示在无限小时间dt内，跑了无限小的距离dx，两者的比值就是瞬时速度V。

比照公式1、2，公式6也可以变化成

dx=Vdt 公式7

五、微分、导数

把公式6与公式1、4比较，可以看出，公式6情况发生了根本性的变化。使用的符号不一样了，含义不一样了，称呼自然也得改变。

1、处于公式7中被乘数位置的V，也即公式6中的分数值，现在称为导数。导数，顾名思义，为了帮助记忆，在这里可以简单理解为推导出来的数。

2、无限小时间dt称为时间t的微分

微即微小之意，分即分割之意，就是把有限大小的值分割成无穷多个无穷小，这个无穷小称为微分。

打个粗略的比方。吃西安羊肉泡馍时，需要把一个完整的面饼掰成很小的小块。我在西安初次吃泡馍时，认为面饼已经掰得很小了，结果老板还是说太大了，需要耐着性子，把面饼掰成很小很小的小块，这样泡出的面饼才好吃。如此尽量小的面饼块就可以看做是面饼的微分。

吃泡馍时把大块面饼微分（掰碎）是为了好吃，数学、物理上把一个量微分是为了好计算。

3、同理，无限小距离dx称为距离x的微分。

六、举例：力学中功的计算

1、对大小、方向均不变化的恒力F

如图1所示，恒力F对物体所作的功A，等于力与物体沿力的方向所作位移大小Δr的乘积。即

A=FΔr （公式8）

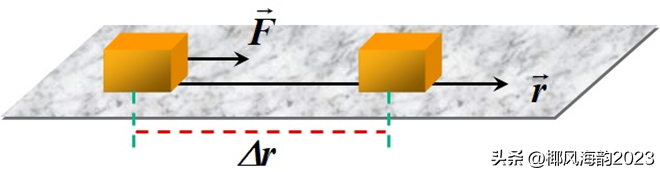
图1 恒力对物体作功

2、对大小或方向随时间变化的变力F

如图2所示，此时，公式8无法直接使用。

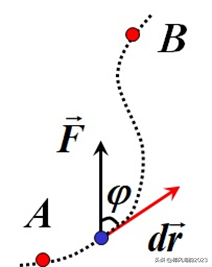
图2 变力对物体作功

此时，就需要微分登场了：可以在物体运动轨道上任取一位移微元dr（微元即微分的意思），在这个位移微元内，近似认为力的大小、方向均不随时间变化，是恒力，则力作的功微元dA：

dA=Fcosφdr （公式9）

（将上式两边积分，就可以得到变力F所做总功。有关积分的具体内容在下一篇中介绍。）

七、函数、自变量

在你跑步时，一般情况，跑的时间越多，跑的距离越长。也就是说，跑的距离是随时间变化的，我们称距离是时间的函数，记为x=f(t)。

“函”字在这里有包含、容纳之意；符号f来自英语词汇function（函数）的第一个字母；

时间t称为自变量，即时间t自己变化，包含时间的距离x随之变化。公式6也可写成

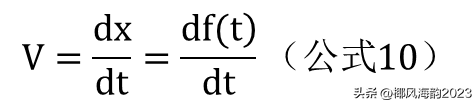
上式称作对函数f(t)求导，或者函数f(t)对t求导，或者f(t)对t的导数是V。

八、极限

在具体求导计算中，自变量无穷小dt可以看做是：有限小Δt趋于零，则公式10可以改写成：

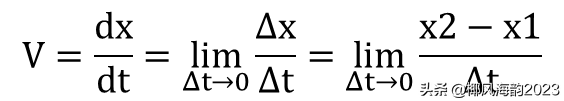
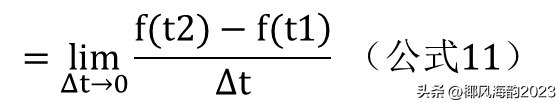
其中，lim是英文词汇limit（意思是极限）的缩写。上式表示的极限就是起跑时的瞬时速度，也就是跑步时间趋于零时跑步速度的值。

九、求导例题

求函数f(t)=t平方的导数。

解：由以上论述，得知

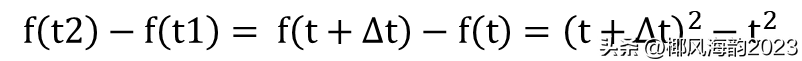
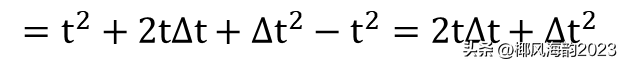
根据公式10和11，导数

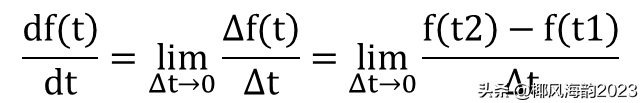
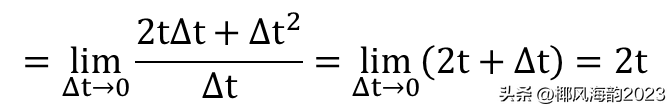
即函数t平方的导数是2t。

这个结果可以作为导数公式记忆下来，还有其他常用导数公式也要背熟，在以后计算中可以直接使用。